Data Science Magic

Your First Machine Learning Project: Predicting House Prices with Ease

Welcome back to another edition of our exciting CodeCraft newsletter! This time, we’re delving into the fascinating world of data science and machine learning. If you've ever wondered how computers can make predictions, recognise patterns, and even make decisions, then this post is for you. Let's dive into the basics of data science and machine learning with Python and explore how you can start building your own intelligent systems. 🤖📊

What is Data Science?

Data science is a multidisciplinary field that combines statistical analysis, data visualisation, and advanced computational techniques to extract meaningful insights from data. It involves collecting, cleaning, analysing, and interpreting large amounts of data to make informed decisions and predictions. Data scientists use a variety of tools and techniques, including machine learning, to uncover patterns and trends hidden in data.

How is Data Science Related to Machine Learning?

Machine learning (ML) is a subset of artificial intelligence that focuses on building systems that can learn from and make decisions based on data. Instead of being explicitly programmed to perform a task, these systems use algorithms to analyse data, learn from it, and make predictions or decisions. Machine learning is a critical component of data science, enabling automated and scalable analysis of complex datasets.

Getting Started with Machine Learning

To get started with machine learning, you'll need a few essential tools:

• Python: Our favorite programming language for data science.

• Libraries: scikit-learn, pandas, numpy, and matplotlib.

A Simple Example: Predicting House Prices

Let's walk through a simple machine learning example: predicting house prices based on features like the number of bedrooms, square footage, and location.

Structure of house_prices.csv

The house_prices.csv file contains data about house sales. Here are the columns in this file:

1. id: A unique identifier for each house.

2. bedrooms: The number of bedrooms in the house.

3. bathrooms: The number of bathrooms in the house.

4. square_footage: The total square footage of the house.

5. location: The location of the house (e.g., 'downtown', 'suburbs', 'rural').

6. price: The sale price of the house.

Sample Data

Here’s an example of how the data might look:

id,bedrooms,bathrooms,square_footage,location,price

1,3,2,1500,downtown,450000

2,4,3,2000,suburbs,600000

3,2,1,900,rural,200000

4,3,2,1600,downtown,475000

5,4,3,2200,suburbs,620000

Step-by-Step Guide

Step 1: Importing Libraries

First, let's import the necessary libraries:

import pandas as pd

import numpy as np

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

import matplotlib.pyplot as plt

Step 2: Loading the Data

Assume we have the dataset house_prices.csv:

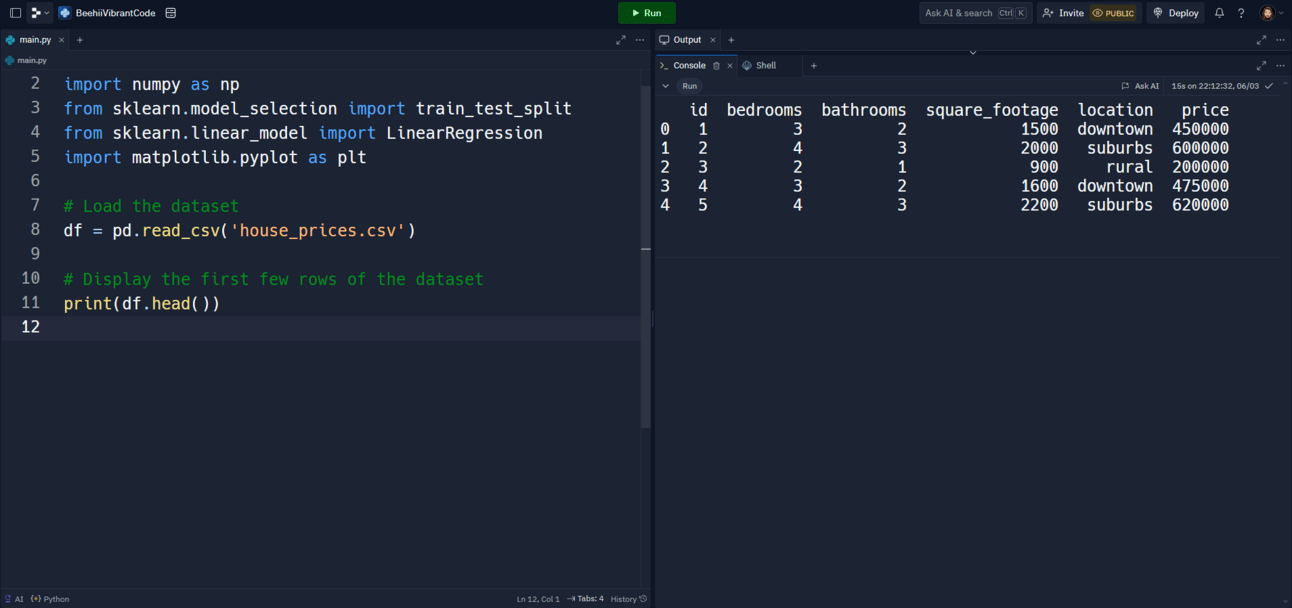
# Load the dataset

df = pd.read_csv('house_prices.csv')

# Display the first few rows of the dataset

print(df.head())

Output

Step 3: Preparing the Data

We need to prepare the data by selecting the features (X) and the target variable (y):

# Select features and target variable

X = df[['bedrooms', 'square_footage', 'location']]

y = df['price']

# Convert categorical data to numerical

X = pd.get_dummies(X, columns=['location'], drop_first=True)

Step 4: Splitting the Data

We split the data into training and testing sets:

# Split the data into training and testing sets

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Step 5: Training the Model

Now, we train a linear regression model:

# Create and train the model

model = LinearRegression()

model.fit(X_train, y_train)

Step 6: Making Predictions

We use the trained model to make predictions on the test set:

# Make predictions on the test set

y_pred = model.predict(X_test)

# Display the first few predictions

print(y_pred[:5])

Output

The number 570000. indicates the first prediction from the model. The model predicts that the first house in the test set should cost around $570,000.

Step 7: Evaluating the Model

Finally, we evaluate the model's performance:

# Evaluate the model

plt.scatter(y_test, y_pred)

plt.xlabel('Actual Prices')

plt.ylabel('Predicted Prices')

plt.title('Actual vs Predicted Prices')

plt.show()

from sklearn.metrics import mean_squared_error

mse = mean_squared_error(y_test, y_pred)

print(f'Mean Squared Error: {mse:.2f}')

Step 7: Evaluating the Model

Evaluating a machine learning model is crucial to understand how well it performs on unseen data. In this step, we use two methods to evaluate our linear regression model: a scatter plot and the model's accuracy score.

Scatter Plot: Actual vs. Predicted Prices

# Evaluate the model

plt.scatter(y_test, y_pred)

plt.xlabel('Actual Prices')

plt.ylabel('Predicted Prices')

plt.title('Actual vs Predicted Prices')

plt.show()

Output Explanation:

• Scatter Plot: The scatter plot visually represents the relationship between the actual house prices (`y_test`) and the predicted house prices (`y_pred`) from our model.

• X-Axis (Actual Prices): This axis represents the actual house prices from the test set.

• Y-Axis (Predicted Prices): This axis represents the house prices predicted by our model.

• Data Points: Each point on the scatter plot corresponds to a house. The position of the point shows the actual price on the x-axis and the predicted price on the y-axis.

• Ideal Line: In an ideal scenario where predictions perfectly match actual values, all points would lie on a diagonal line (y = x). The closer the points are to this line, the better the model's predictions.

By examining this plot, we can visually assess how well our model's predictions align with the actual house prices. Points that are far from the diagonal line indicate larger prediction errors.

Model Accuracy

The code snippet below is to be added before the plt.show() .

# Calculate the Model Accuracy

accuracy = model.score(X_test, y_test)

print(f'Accuracy: {accuracy:.2f}')

Output Explanation:

• Accuracy Score: The model.score(X_test, y_test) function calculates the R^2 score (coefficient of determination) of the prediction.

• R^2 Score: This score represents the proportion of the variance in the dependent variable (house prices) that is predictable from the independent variables (features such as bedrooms, square footage, and location).

• Range: The R^2 score ranges from 0 to 1. A score closer to 1 indicates that a large proportion of the variance in the dependent variable is explained by the model, while a score closer to 0 indicates that the model does not explain much of the variance.

For example, if the output is:

Accuracy: 0.97

This means that our model explains 97% of the variance in house prices based on the features provided. An accuracy score of 0.97 is generally considered good, indicating that the model makes reasonably accurate predictions.

(Note: The output below was produced using a set of 30 house prices data. If there is insufficient data, the score will not be well defined or cannot be calculated.)

Summary

• Scatter Plot: Helps visualise the accuracy of the model's predictions against actual prices.

• R^2 Score: Provides a numerical measure of the model's predictive power.

By using these evaluation methods, we can better understand the performance of our machine learning model and identify areas for potential improvement.

Conclusion

And there you have it! You've just built a simple machine learning model to predict house prices. Machine learning is a powerful tool, and this is just the tip of the iceberg. Stay tuned for more exciting tutorials where we'll dive deeper into various machine learning algorithms, data preprocessing techniques, and advanced topics like deep learning.

Ready for More Python Fun? 📬

Subscribe to our newsletter now and get a free Python cheat sheet! 📑 Dive deeper into Python programming with more exciting projects and tutorials designed just for beginners.

Keep exploring, keep coding, 👩‍💻👨‍💻and enjoy your journey into data analytics with Python!

Happy coding!🚀📊✨